- NÚMEROS ENTEROS
- Número entero,es cualquier elemento del conjunto formado por los números naturales y sus opuestos. El conjunto de los números enteros se designa por Z:Z = {…, -11, -10,…, -2, -1, -0, 1, 2,…, 10, 11,…}

- REGLAS DE LOS SGNOS
12 -multiplicar
a)*(+10).(-2) =-20
 Ejercicios a)[(+60):( -30)]:(-2)=[-2]:(-2) =-2/-2 =+1
Ejercicios a)[(+60):( -30)]:(-2)=[-2]:(-2) =-2/-2 =+1
Si se multiplican los dos miembros de una fracción
por el mismo numero,se obtiene una fraccion equivalente :
a/b=a.n/b.n
Si se dividen los términos de unas fracción por el mismo
b)*(-4).(-9)= 34
c)*(-7).(+5) = 35
d)*(+11).(+7)=77
14-Divider
a)*(-18):(+3)=-54
b)*(-15):(-5) =3
c)*(+36):(-9)=-4
d)*(-30):(-10)=3
 Ejercicios a)[(+60):( -30)]:(-2)=[-2]:(-2) =-2/-2 =+1
Ejercicios a)[(+60):( -30)]:(-2)=[-2]:(-2) =-2/-2 =+1 - FRACCIONES EQUIVQLENTES
como reconocer fracciones equivalentes ?
EN las fracciones equivalentes ,los prod-
uctos de los términos cruzados
- Propiedad fundamental de las fracciones
Si se multiplican los dos miembros de una fracción
por el mismo numero,se obtiene una fraccion equivalente :
a/b=a.n/b.n
Si se dividen los términos de unas fracción por el mismo
numero ,se obtiene una fracción equivalente :
a/b=a:n/b:n
b
Esta transformación recibe el nombre de simplificación de fracciones.
Una fraccion que no se puede simplificar llama irreducble
EJEMPLOS
12/30=12:2/30:2=6/15=6:3/15:3=2/5 -Fraccion irreducible
 PROPORCIONALIDAD DIRECTA
PROPORCIONALIDAD DIRECTA
onsiste en que dadas dos cantidades correspondientes a magnitudes directamente proporcionales, calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.


MULTIPLICACION :Se deja como base lo mismo y se suman los exponentes .

DIVICION:se deja como base el mismo numero y se restan los exponentes.
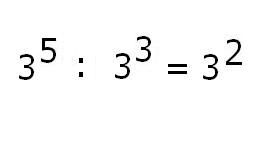
-DEFIRENTES BASES
MULTIPLICACIONES :Se multiplican las dos bases y se deja igual el expenente
Ejemplo :
-DIVISION :Se dividen las dos bases y se deja
igual el exponente
Ejemplos ;

EJEMPLOS
12/30=12:2/30:2=6/15=6:3/15:3=2/5 -Fraccion irreducible
onsiste en que dadas dos cantidades correspondientes a magnitudes directamente proporcionales, calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.

La regla de tres directa la aplicaremos cuando entre las magnitudes se establecen las relaciones:
A más  más.
más.
 más.
más.
A menos  menos.
menos.
 menos.
menos.Ejemplos
Un automóvil recorre 240 km en 3 horas. ¿Cuántos kilómetros habrá recorrido en 2 horas?
Son magnitudes directamente proporcionales, ya que a menos horas recorrerá menoskilómetros.
240 km 3 h
3 h
 3 h
3 h
x km  2 h
2 h
 2 h
2 h
Ejemplo
*Por revelar 41 fotografías nos han cobrado 8,2 €. ¿Cuánto nos costará
revelar 22 fotografías?
41--------------8,2
22--------------X
X=22.8,2
41
X=4.4
150-----------24
30------------x
X=30.24
150
X=4.8
el aciete dura para 180 alimnos
*24-4.8=
- potencias
MULTIPLICACION :Se deja como base lo mismo y se suman los exponentes .

DIVICION:se deja como base el mismo numero y se restan los exponentes.
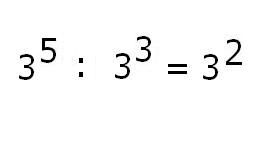
-DEFIRENTES BASES
MULTIPLICACIONES :Se multiplican las dos bases y se deja igual el expenente
Ejemplo :
igual el exponente
Ejemplos ;
- ECUACIÓN
Ecuaciones de primer grado
Ecuaciones de primer grado, ejemplos y ejercicios resueltos de ecuaciones con paréntesis y denominadores.
Matemáticas 3º de ESO 6.1 Ecuaciones de primer grado. Ejemplos
Concepto de ecuación
Para que exista una ecuación tiene que haber algo igual a algo. Una ecuación es de primer grado cuando la x (la variable) está elevada a uno.Pasos para resolver una ecuación de primer grado
1. Si hay denominadores, los reducimos a común denominador (calculando el m.c.m ) y suprimimos los denominadores.2. Quitamos los paréntesis aplicando la regla de los signos. Al final tendremos a ambos lados del igual, sólo sumas y restas, unos términos llevaran x y otros no.3. Trasposición de términos: Pasamos todos los términos con x a un lado de la ecuación, los números al otro lado.4. Agrupamos los términos semejantes y al final despejamos la x obteniendo la solución.5. Comprobamos la solución sustituyendo el valor de la x obtenida en la ecuación. Nos tiene que dar el mismo resultado a ambos lados de la ecuación.Soluciones de una ecuación de primer grado. Ejemplos
Un número real: es cuando normalmente decimos que nos da solución.x + 3 = 5 x + 11 ⇒ x - 5 x = 11 - 3 ⇒ - 4 x = 8 ⇒ x = 8 / - 4 ⇒ x = - 2Todo número real: nos da ⇒ 0 x = 0. Tiene solución para cualquier valor de x, decimos que tiene infinitas soluciones.13 - 3 x - 9 = 8 x + 4 - 11 x ⇒ - 3 x - 8 x + 11 x = 4 + 9 - 13 ⇒ 0 = 0Incompatible: se anulan las x y nos da ⇒ 0 x = número. No tiene solución.6 + 5 x + 2 = 4 x - 2 + x ⇒ 5 x - 4 x - x = - 2 - 6 - 2 ⇒ 0 x = - 10- Ejercicios resueltos

No hay comentarios:
Publicar un comentario